前節<(学習の目的)
国民所得がどうやって決まるか、一番かんたんな形のモデル(※)をまなびます。
※「モデル」とは、「なぜ?」について原因や理由を説明する考え方の「枠組み」です。
- はじめは政府や海外貿易を考えない、もっともかんたんなモデルをみていきます。
需給均衡式
- もっとも単純なモデルでは、政府と海外貿易が無いと仮定します。
- 「三面等価の原則」から、生産面つまり「総供給」と、支出面つまり「総需要」は等しくなります。
- 需要と供給が等しい(均しい)ので、「需給が均衡」している状態です。
(総供給)
総供給は「Y」で表します。
- これは生産された付加価値です。
- この付加価値は人々の所得として分配され、人々はそのお金を支出して、他人の作り出した付加価値を手に入れます。
- この使い方を「総供給」として表します。
(総需要)
総需要は「消費」(C)と「投資」(I)で構成されます。
- 買って使ったら消えてしまうものが消費です。
- 新たな生産のために必要なものを買うために使うのが投資です。
この総供給と総需要は等しくなり、次の形で表されます。
Y = C + I
この式を「需給均衡式」といいます。
国民所得と消費の関係
- 「不景気」とは、国民所得が増えなかったり減少したりする状態です。
- なぜ不景気になるかというと、消費が少ないからです。
- これは「消費(I)→国民所得(Y)」の関係です。
- でも、なぜ消費が少ないかというと、不景気だからです。
- これは「国民所得(Y)→消費(I)」の関係です。
- つまりこの「消費」(I)と「国民所得」(I)は、お互いに影響を与え合っているのです(※)。
- ※このように、お互いに影響を与え合うものを「内生(変数)」といいます。
消費関数
- この「国民所得(Y)→消費(I)」の関係は、「消費関数」として式で表現できます。
消費関数は次の形で表します。消費は「Consumption」ですので、記号は「C」で表すのがふつうです。
C = C0 + c1・Y
消費 = 基礎消費 + 限界消費性向×国民所得
基礎消費と限界消費性向
- 所得の大小とは関係なく必要となる消費を「基礎消費」といいます。ここでは「C0」とします(他の記号でも構いません)。
- 所得が1単位増加したときの消費の増加分を「限界消費性向」といいます。ここでは「c1」とします(これも他の記号でも構いません)。
- イメージとしては、「手に入ったお金の何%を使うか?」を表したものです。
- この「限界消費性向」の値は、全く使わない「ゼロ」よりは大きくて、全部使ってしまう「1」よりは小さくなります。
- だから、式と一緒に「0<c1<1」と書いておくといいでしょう。
次は、消費に続いて、投資につてみていきましょう。
投資の仮定
- 投資についても、消費関数のように「投資関数」を作ることができます。
- でも、ここではモデルをかんたんにするために、投資は一定と仮定します。
- 計算問題では、たとえば「I=100」などの具体的な数字の形で与えられます。
- 記号で表す場合は、「I」の上に「-」(バー)をつけて表したりします(ここでは「I0」であらわします)(※)。
- ※このような定数を「外生(変数)」といいます。
連立方程式を解く
ここまでで、2つの式が出てきました。
①需給均衡式 Y = C + I
②消費関数 C = C0 + c1・Y (0<c1<1)
- 両方の式で「Y」(国民所得)と「C」(消費)が示されています。
- 両方とも変数(方程式のXやYなど)を表していますので、これらは「連立方程式」です。
- 「国民所得」(Y)の値を求めるためには、「Y」とは別の「C」を消します。
よって、実際の計算は、
①需給均衡式「Y=C+I」に
②消費関数 「C=C0+c1・Y」
を代入して求めます。
(正確には、投資「I」に定数として与えられた数値を代入します。ここでは「I0」を代入します。)
式の展開
Y=C+I
に、「C=C0+c1・Y」の右辺を代入するとこうなります。
Y=C0+c1・Y+I0
「Y」がついているものは左辺にまとめてしまいましょう。
Y-c1・Y=C0+I0
左辺を「Y」でくくるとこうなります。
Y(1-c1)=C0+I0
「Y」の値を求めるために、両辺を(1-c1)で割りましょう。
Y = 1/(1-c1)・(C0+I0)
ところで、この国民所得(Y)は、総需要と総供給が均衡した状態の「均衡国民所得」ですから、「Y」の右上に「*」(アスタリスク)をつけて、「Y*」の形で表しておきましょう。
Y* = 1/(1-c1)・(C0+I0)
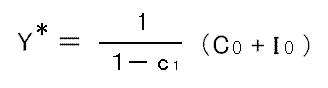
これが均衡国民所得の求め方です。
→ 次は「乗数効果」です。「~を増やしたら国民所得がどれだけ増えるか」を示したものです。
1.財市場
│国民所得とは何か?│三面等価の原則│有効需要の原理│国民所得の決定│乗数効果│「45度線」分析│インフレ・ギャップとデフレ・ギャップ│政府部門と海外部門をふくむモデル│