2-1.生産関数 < 2-2.費用最小化の条件 > 2-3.総費用
(学習の目的)
ここの説明の方法は、消費者理論の「無差別曲線と予算制約線」と同一です。 ここで学ぶ「費用最小化の条件」と、次の章の「利潤最大化の条件」は区別が必要です。
生産関数
(1)でまなんだ生産関数は、「資本」もしくは「労働」のそれぞれの投入量と「生産量」の関係をあらわしたものでした。ここでは、「資本」と「労働」の投入量の組合せと「生産量」を結びつけて生産関数を描きます。
等量曲線
- 2つの生産要素の組合せについて描いた生産曲線を「等量曲線」(等産出量曲線)といいます。
- この曲線は、「同じ生産量を生産するのに必要な生産要素の組み合わせ」を示したものです。
- 消費者理論でまなんだ「無差別曲線」と同じ分析の方法を用います。
技術的限界代替率
- 「技術的限界代替率」とは、一方の生産要素を1単位増加させたとき、「同じ生産量」を保つために、もう一方の生産要素を「何単位減少」させるべきかを示したものです。
- 計算問題で求める場合、この「技術的限界代替率」は「限界生産力の比」に等しくなります。
- 正確には、「資本の限界生産力」と「労働の限界生産力」の比になります。
- 一般的に、等量曲線の形は、「原点に対して凸型」になります。
- これは、「技術的限界代替率逓減の法則」があてはまるケースです。
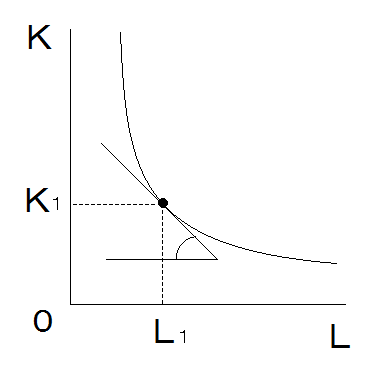
コブ=ダグラス型生産関数
この「原点に対して凸型」の等量曲線(生産関数)は、一般的に「コブ=ダグラス型生産関数」の形であらわされます。
- 生産量を「Ⅹ」、資本を「K」、労働を「L」とすると、この関数は次の形であらわされます。
X=KαLβ - 「K」と「L」の右上についている「α」と「β」は「指数」です。「指数」は、「2乗」などの「n乗」の形であらわされます。
- 「コブ=ダグラス型生産関数」では、この「α」や「β」は分数や小数の形であらわされ、「α+β=1」となるのが一般的です。
- ただ、この式はやや難しいので、今は「原点に対して凸型」の等量曲線のことを「コブ=ダグラス型生産関数」ということを確認しておいてください。
レオンチェフ型生産関数
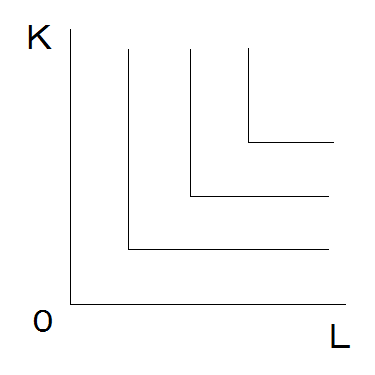
「無差別曲線」と同じように、「原点に対してL字型」の等量曲線も描けます。
- このような形の等量曲線(生産関数)を「レオンチェフ型生産関数」といいます。
- これは、ある生産量を生産するために必要な「資本」と「労働」には、一定の組合せがあることを示しています。
- グラフでは、「L」字型の角の部分がその組合せを示しています。
- さきほどの「コブ=ダグラス型生産関数」では、一定の生産量を生産するために、さまざまな「資本」と「労働」の組合せがあることを示しています。いわば柔軟な生産システムです。
- これに対して、「レオンチェフ型生産関数」は、硬直的な生産システムをあらわしています。
等費用線
- 等費用線」とは、「生産要素の価格」が与えられているとき「同じ総費用」となる生産要素の組み合わせを示したものです。
- これは、消費者理論の「予算制約線」に相当するものです。
- この「等費用線」の傾きは、「生産要素の価格比」になります。
最適生産
企業は「等量曲線」と「等費用線」の「接点」で、費用が最小となる生産要素の最適な投入量を決定します。
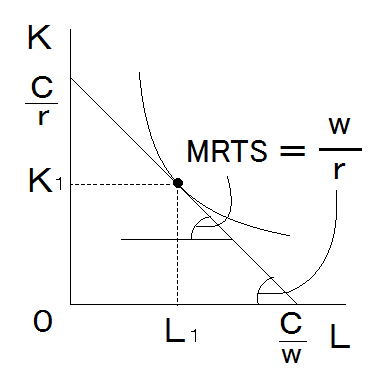
技術的限界代替率 = 生産要素の価格比
(「技術的限界代替率」は「限界生産力の比」から求めます。)
→次は「総費用」です。費用にはさまざまな定義がありますので、まずはここからまなびます。