1-2.無差別曲線 < 1-3.予算制約線 > 1-4.所得の変化
(学習の目的)
予算制約式の立て方を学びます。シフトの理由をマスターしてください。計算問題については1次方程式(直線)の理解が必要です。
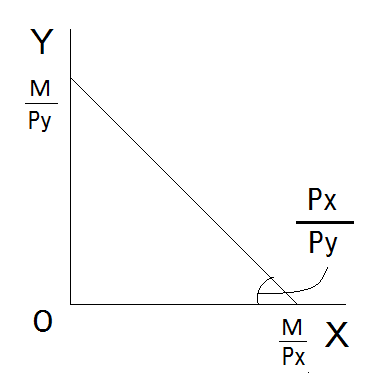
予算制約線
「予算制約線」は、「財の価格」と消費者の「所得」(予算)が与えられているとき、消費者が「最大限に購入可能な財の組合せ」を示します。
- この関係を式であらわしたものが「予算制約式」です。
- 「予算制約線」の「傾き」は、財の「価格比」になります。
- 「予算制約線」の「切片」は、「所得」を財の価格で割って求められます。
- 横軸の切片は、「所得」を横軸の財の価格で割って求めた財の消費量になります。
- 縦軸の切片は、「所得」を縦軸の財の価格で割って求めた財の消費量になります。
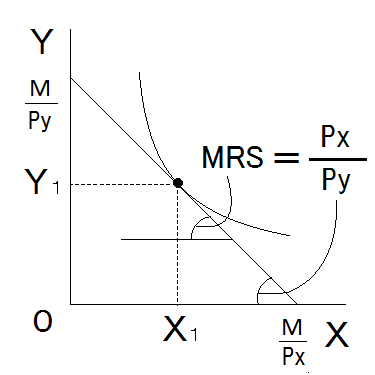
最適消費点
消費者は、与えられた「所得」(予算)制約の下で、自分の「効用」を最大化しようとします。
- この関係は、「無差別曲線」と「予算制約線」を結びつけることであらわすことができます。
- 「無差別曲線」と「予算制約線」の「接点」では、効用が最大となる「最適消費量」が決定されます。
- このような「無差別曲線」と「予算制約線」の「接点」を「最適消費点」といいます。
効用最大化の条件
「最適消費点」では、「予算制約の下で効用が最大化」されております。このような状態(効用最大化)になる条件は、次の形であらわされます。
(効用最大化の条件)
限界代替率 = 価格比
「限界代替率」は、「限界効用の比」で求められるので、こう書きかえることができます。
限界代替率 = 限界効用の比 = 価格比
これで、一定の予算のもとで、価格が与えられたときに、効用が最大となる消費量(需要量)を求めることができます。
(次の考察)価格が変化すると消費量も変化することになるのですが、その前に、所得(予算)が変化するとどうなるかをみていきます。
→ 次は「所得の変化」です。予算制約線が平行シフトします。