1-1.限界効用 < 1-2.無差別曲線 > 1-3.予算制約線
(学習の目的)
2つの財の消費量の組合せでグラフを描きます。等高線をイメージしてください。
〔ミクロ1-2〕無差別曲線
0:00 はじめに / 0:36 無差別曲線 / 1:29 無差別曲線の性質 / 4:22 限界代替率 / 5:05 限界代替率の計算方法 / 5:24 限界代替率逓減の法則
※ 無差別曲線のイメージをつかむためにはこちらの動画をどうぞ。
無差別曲線
- (1)でまなんだ「効用曲線」は、ある財の「消費量」と「効用」の組合せを示したものでした。
- 次に、2つ財の「消費量」の組合せで「効用曲線」をえがきます。これが「無差別曲線」です。
- 「無差別曲線」とは、ある消費者にとって「等しい効用がえられる2つの財の消費量の組合せ」をつないだ曲線のことです。
- 地形図の等高線をイメージしてください。
無差別曲線の性質
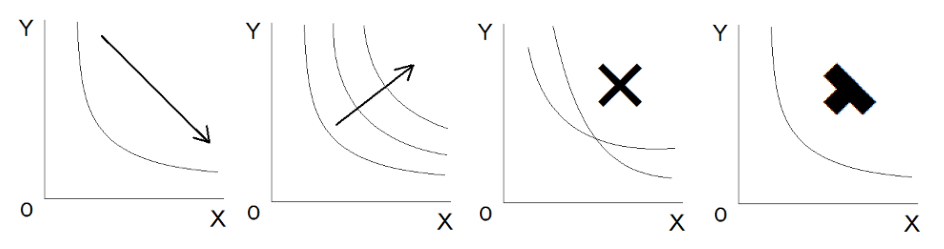
この「無差別曲線」には、以下の4つの性質があります。
- 「右下がり」である。これを代替性(単調性)の仮定といいます。
- 「右上ほど効用が高い」。これを非飽和の仮定といいます。
- 「互いに交わらない」。これを推移律の仮定といいます。
- 「原点に対して凸」。これを「限界代替率逓減の法則」といいます。
限界代替率
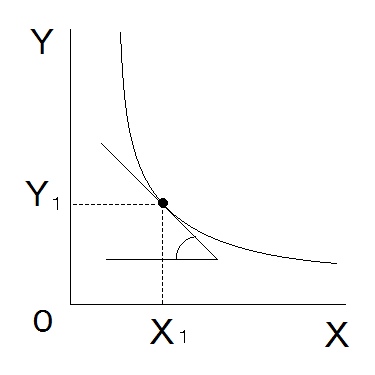
「限界代替率」とは、ある財の「消費量を1単位増加させたとき、同じ効用を保つために、もう一方の財を何単位減少させればよいか」を示します。
- 「限界代替率」をグラフであらわすと、「無差別曲線」上の点に引いた「接線の傾き」になります。
- なお、「限界代替率」については計算問題でもよく出題されます。これは「限界効用の比」を求めることで導き出すことができます。
限界代替率逓減の法則
一般的な「無差別曲線」は、原点に対して凸型の形であらわされます。
- これは、「限界代替率逓減の法則」があてはまっている状態です。
- 「限界代替率逓減の法則」とは、「財の消費量が増加するにしたがって、限界代替率が徐々に小さくなること」をいいます。
- この性質があてはまるとき、無差別曲線は原点に対して凸型になります。
- 無差別曲線は(7)でまなぶように、さまざまな形がありますが、原点に対して凸でないものは、この「限界代替率逓減の法則」があてはまらないものです。
関連動画「限界代替率とは?」
(練習問題)ある個人の効用関数 U=X・Y (U:効用、X:X財の消費量、Y:Y財の消費量) について、この曲線上の点における限界代替率の求め方を示してください。
→ 次は「予算制約線」です。買い物には予算が大切です。