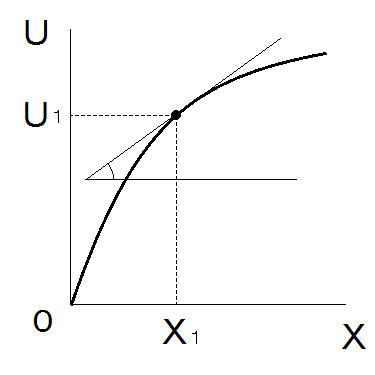1-1.限界効用 > 1-2.無差別曲線
(学習の目的)
人間の行動理由である「欲望」を「効用」と定義して分析します。また、経済学でよくつかう「限界」という考え方を知ります。限界とは微分のことだと思ってください。
効用
- 消費者が財・サービスを購入して得られる満足感を「効用」といいます。
- この消費者の行動目標は、一定の「予算制約」のもとで、「効用の最大化」をはかることです。
- 財の消費量と効用の関係を表す関数を「効用関数」といいます。
- 横軸に財の消費量、縦軸に効用をとって、両者の関係を示したグラフを「効用曲線」といいます。
- このグラフの形は「右上がり」です。これは「消費量が増えるほど効用も増える」ことを仮定しているからです。「飽きることがない」ので、「非飽和の仮定」といいます。
限界効用
- 「財の消費量が1単位増加したときに得られる効用の増加分」を「限界効用」といいます。
- 「効用関数」を用いた数式では、この「限界効用」は、「効用を消費量で微分」して求められます。
- なお、「効用関数」をグラフにした「効用曲線」で示すと、「限界効用」はグラフ上の点に引いた「接線の傾き」になります。
- 一般的に効用曲線の形状は上に凸型です。消費量が増えるほど「効用」は増えますが、その増え方はだんだんゆるやかになっていきます。
- これは日常的な感覚から導かれた法則で、「限界効用逓減の法則」といいます。
→ 次は「無差別曲線」です。財が2つになるのが特徴です。
1-1.限界効用 > 1-2.無差別曲線