3-4.課税と規制の影響 < 4-1.パレート効率性 > 4-2.厚生経済学の基本定理
(学習の目的)
効率的な資源配分の状態を定義します。
一般均衡分析と部分均衡分析
前章でまなんだ「部分均衡分析」も、本章の「一般均衡分析」も、ともに「最適な資源配分」について分析する方法です。
- 「部分均衡分析」は、「1つの財」を取り上げて、需要曲線と供給曲線をえがいて説明しました。
- これに対して、「一般均衡分析」では、「複数の財」を取り上げて分析します。
- 具体的には、「無差別曲線」と「予算制約線」を用います。
パレート効率的資源配分
ここでは、「最適な資源配分」として、「効率的な資源配分」を定義します。
- この「効率的な資源配分」を「パレート効率的」資源配分といいます。
- この資源配分は「社会」全体からみて望ましい状態のことです。
- 個人としては、自分の効用「だけ」が最大化になれば、それが最適な状態です。でも、現実には、「他者」がいます。
- 時として、他人に影響を与えることなく、自分の効用を増やすことができるかもしれません。
- でも、いずれは、他人の効用が邪魔になる場合があります。
- このようなギリギリの状態を次のように定義し、「社会」全体からみて最も望ましい状態と考えます。
「パレート効率的」資源配分とは、「他の人の効用を減少させないことには、ある人の効用を増加させることができない」状態のことをいいます。
パレート改善
- さきほど、「他人に影響を与えることなく、自分の効用を増やすことができる」状態を取り上げました。
- これが「パレート改善」です。
「パレート改善」とは、「他の人の効用を減少させずに、ある人の効用を増加させることができる」変化のことをいいます。
ボックス・ダイアグラム
この「パレート効率的」な資源配分を説明するためには、「自分の効用」と「他者の効用」という2人分の効用を合わせて考察する必要がでてきます。
- これをあらわしたのが、「エッジワースのボックス・ダイアグラム」です。
- 「エッジワースのボックス・ダイアグラム」では、2人の個人の無差別曲線を1つの図にまとめます。
- 描き方は次の通りです。
- まず、「ボックス・ダイアグラム」の名前の通り、「箱」を描きます。
- 横軸はある財の「存在する量」で、縦軸は別の財の「存在する量」とします。
- そして、左下の原点を基準として、ある人の無差別曲線をえがきます。
- また、右上を原点として別の人の無差別曲線を描きます。
パレート改善の図示
この両者の無差別曲線はいくつかの描き方があります。
- まず、交わって描かれる場合をみていきます。
- この場合、一方の無差別曲線はそのままにしておいて、もう片方はより効用の高い無差別曲線上で消費をおこなうことができます。
- これは、「他の人の効用を減少させずに、ある人の効用を増加させることができる」変化ですから、「パレート改善」です。
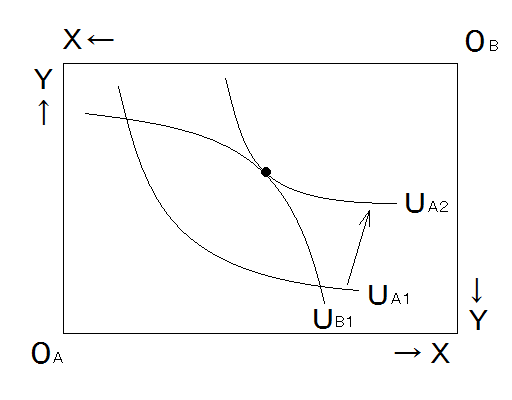
パレート効率的資源配分の条件
- これとは別に、ある人と別の人の無差別曲線が、1点で「接する」状態も描くことができます。
- これは、「他の人の効用を減少させないことには、ある人の効用を増加させることができない」状態、つまり「パレート効率的」な資源配分が達成されている状態です。
- 「パレート効率的」な資源配分が達成されている状態は、2人の個人の「無差別曲線の接点」になっております。
- この点に接線を引くと、その傾きは等しくなります。
- 「無差別曲線」上の点に引いた接線の傾きは「限界代替率」ですので、「パレート効率的資源配分の条件」として、次の関係が導き出されます。
ある個人の限界代替率 = 他の個人の限界代替率
契約曲線
- この2人の個人の「無差別曲線の接点」の組合せは複数あります。
- これらの「パレート効率的」な資源配分がなされる点を結んだ曲線を「契約曲線」といいます。
純粋交換経済
- ここで説明した「エッジワースのボックス・ダイアグラム」は、正確に言えば、2人の消費者がお互いの財を交換し合う「純粋交換経済」を想定しております。
→次は「厚生経済学の基本定理」です。価格調整による資源配分をみていきます。
3-4.課税と規制の影響 < 4-1.パレート効率性 > 4-2.厚生経済学の基本定理