1-8.消費者理論の応用 < 2-1.生産関数 > 2-2.費用最小化の条件
(学習の目的)
「限界生産力」という考え方を理解します。これはマクロ経済学でも使う重要な考え方です。
生産要素
財を生産するためには、「資本」「労働」「土地」の3つの「生産要素」が必要です。
- この中で、「土地」については議論がややこしくなるので、ここでは除外して考えます。
- つまり、「資本」と「労働」を組み合わせて、財を生産すると考えるのです。
生産関数
生産要素の投入量と生産量の関係をあらわしたものが「生産関数」です。
- 生産要素は「資本」と「労働」の2つにわけることができますので、「資本」と「生産量」の生産関数と、「労働」と「生産量」の生産関数の2種類が求められます。
- 「資本」についてみるときは、「労働」は一定と仮定します。
- 「労働」についてみるときは、「資本」は一定と仮定します。
- このような仮定をするときは、「他の生産要素を一定として」とあらわします。
生産関数のグラフ
- 生産関数は、生産曲線としてグラフにえがくことができます。
- このグラフの横軸は「資本」もしくは「労働」の投入量で、縦軸は「生産量」になります。
- 形は一般的に上に凸型になります。これは「限界生産力が逓減する」生産関数です。
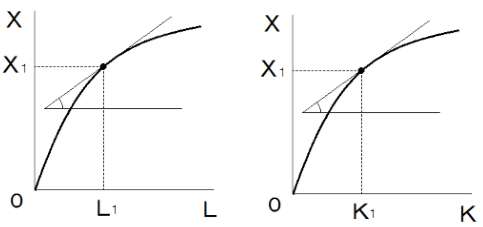
限界生産力
「他の生産要素を一定として」「ある生産要素を1単位増加させたときの生産量の増加分」を「限界生産力」といいます。これは、いわゆる「生産性」のことです。
- 生産要素は「資本」と「労働」の2つに分けられます。
- 「資本」を1単位増加させたときの生産量の増加分を「資本の限界生産力」といいます。
- 「労働」を1単位増加させたときの生産量の増加分を「労働の限界生産力」といいます。
限界生産力の求め方
「生産関数」を用いた数式では、この「限界生産力」は、「生産量を生産要素の投入量で微分」して求められます。
- 「資本の限界生産力」は生産量を「資本」の投入量で微分して求めます。
- 「労働の限界生産力」は生産量を「労働」の投入量で微分して求めます。
- また、「生産関数」をグラフにした「生産曲線」で示すと、「限界生産力」はグラフ上の点に引いた「接線の傾き」になります。
限界生産力逓減の法則
- 生産要素の投入量と生産量の関係を示した生産関数の形は、一般的に「上に凸」型です。
- つまり、生産要素の投入量が増えるほど、限界生産力が徐々に低下していくことをあらわしています。
- これは日常的な感覚から導かれた法則で、「限界生産力逓減の法則」といいます。
規模に関する収穫
ここまでは、「他の生産要素を一定とした」生産関数をみてきました。
次に、「すべての生産要素」を変化させたらどうなるかをみていきましょう。
ここでは、「すべての生産要素をn倍」投入したらどうなるかを考えます。すると、以下の3通りの状況が考えられます。
- 「規模に関する収穫逓増」・・・すべての生産要素をn倍投入したとき、生産量がn倍より大きくなるケース。
- 「規模に関する収穫一定」・・・すべての生産要素をn倍投入したとき、生産量がn倍になるケース。
- 「規模に関する収穫逓減」・・・すべての生産要素をn倍投入したとき、生産量がn倍より小さくなるケース。
→ 次は「費用最小化の条件」です。消費者理論でまなんだ無差別曲線と予算制約線の考え方をつかいます。
1-8.消費者理論の応用 < 2-1.生産関数 > 2-2.費用最小化の条件